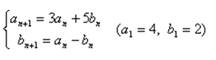
＜連立漸化式の行列を用いた方法＞

 

まず、これらを行列で表現してみよう

　・・・・�@

 

表現を簡単にするために、次のように置いてみる。

 

 ,　  ,   とすると

 

   ・・・・�A

ここに、 　である。

 

�Aは等比数列と形が似ている。

すなわち、帰納的に次のように表せる。(厳密には数学的帰納法を用いて証明する。)

 

…………………………………..

 

 

よって、　　 　　　・・・　�B

である。

 

●  結局、連立漸化式の一般項を求めることは行列のｎ乗を計算することになる。

 

 のｎ乗を計算する。

そこで、行列を対角化することを考える(行列を対角形にするとｎ乗の計算がしやすいので)。

このあたりのことは次のサイトを見てください。

 

●  ＜行列ｎ乗のまとめ＞

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

＜行列の練習問題＞

 

１、　　　の　逆行列が存在するかどうかを判定せよ。

 

 

 

２、行列　　　　　に対して、 ,  

  を満たす行列 を求めよ。（途中経過を記入）

 

 

 

３,   行列 が逆行列をもたないように,の値を定めよ。

（簡単な途中経過を記入）

 

 

４,  次の等式を満たす２次の正方行列 を求めよ。（途中経過を記入）

  ,

 

 

 

５、逆行列を用いて、次の連立方程式を解け。（簡単な途中経過を記入）

（１）

 

（２）

 

 

 

６、次の問いに答えよ。（途中経過を記入）

�@　 のとき、　を求めよ。

 

 

�A　  のとき、 を求めよ。

 

７、次の連立方程式のうち、解を無数にもつものはどれか、解をもたないものはどれか。（理由を付して答えよ）

�@　      

 

 

�A　

 

 

 

８、

 のとき、 とする。　 が対角行列　となることを利用して、 ,  を計算し、 を類推で求めよ。（解答に当たって、 あたりまでは省略せずに書くこと。）

 

 

 

９、２次の正方行列　 の逆行列　 が存在するとき、

　　 が成り立つことを証明せよ。

 

 

 

10、行列   は正方行列、　は 　と　同じ型の単位行列とするとき、

　　 ならば　 は　の逆行列であることを示せ。

 

 

11、連立１次方程式

  が　 以外の解を持つように定数　 の値を定めよ。

（論旨が明確になるように、対偶を用いて解答せよ。）